分類:燒腦題
出自六年制學程
求 a b
a2+b2=20 ,且 b 是 a 的小數部分。
|b|<1 且 b2 < 1
a2 > 19
設 a=n+b n為整數,且必為 ±4
(±4+b)2+b2=20
16±8b+2b2=20 => b2±4b-2=0
b=(∓4±√16+8)/2
b=∓2±√6
|b|<1 ,者 僅有 √6-2 , 2-√6
a=4+b=√6+2 , -(√6+2)
中學數學題
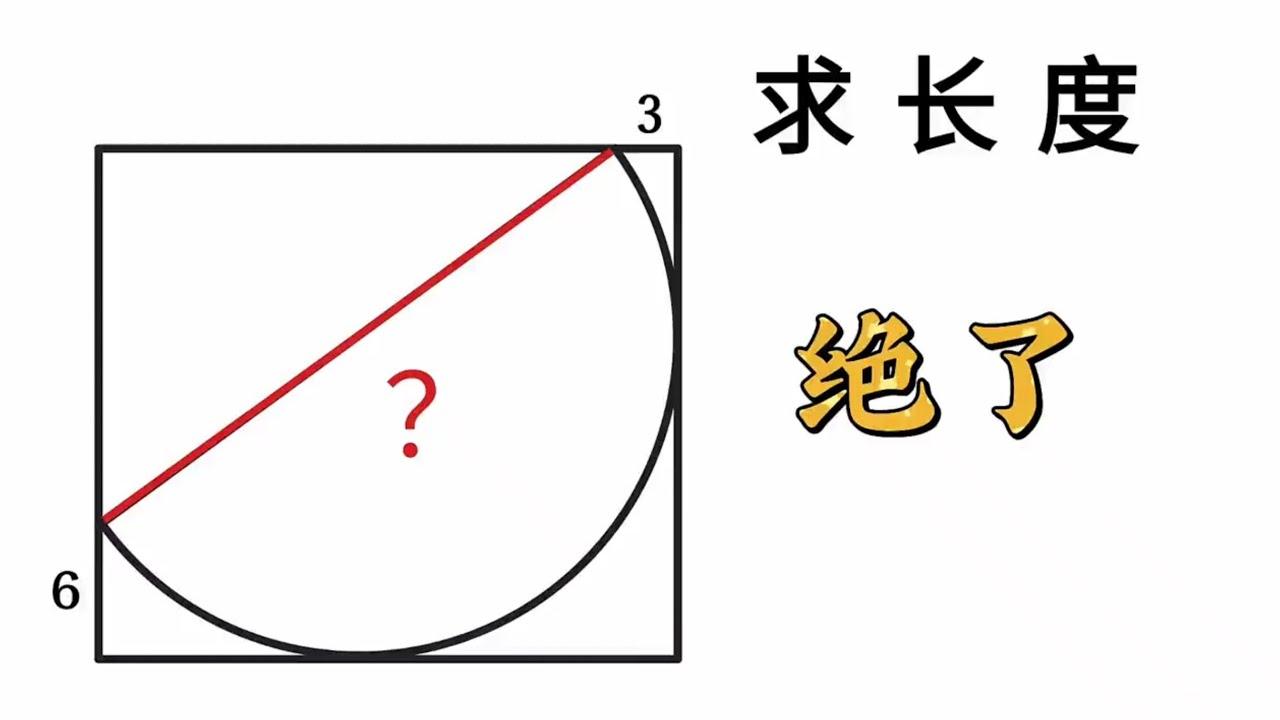
圓相關
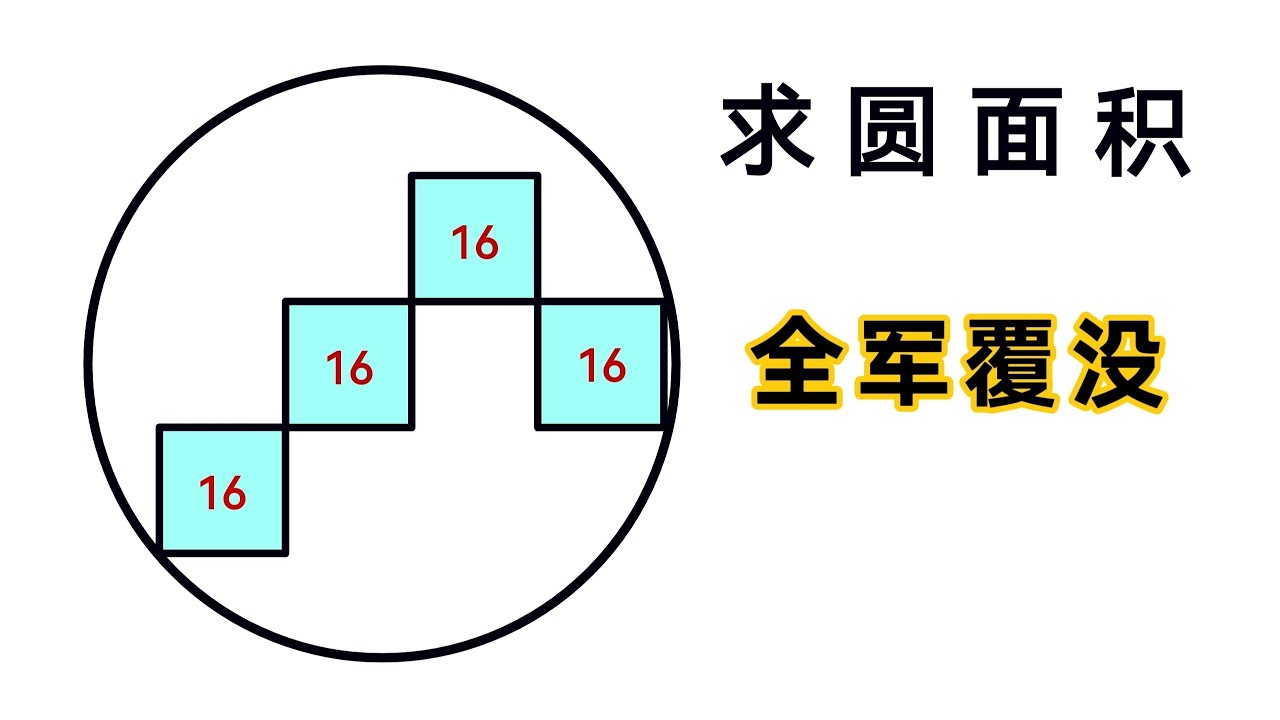
解出三邊為 3.4.5
2,(4-r),(2+r) 構成直角三角形,解出 r 為 4/3 。
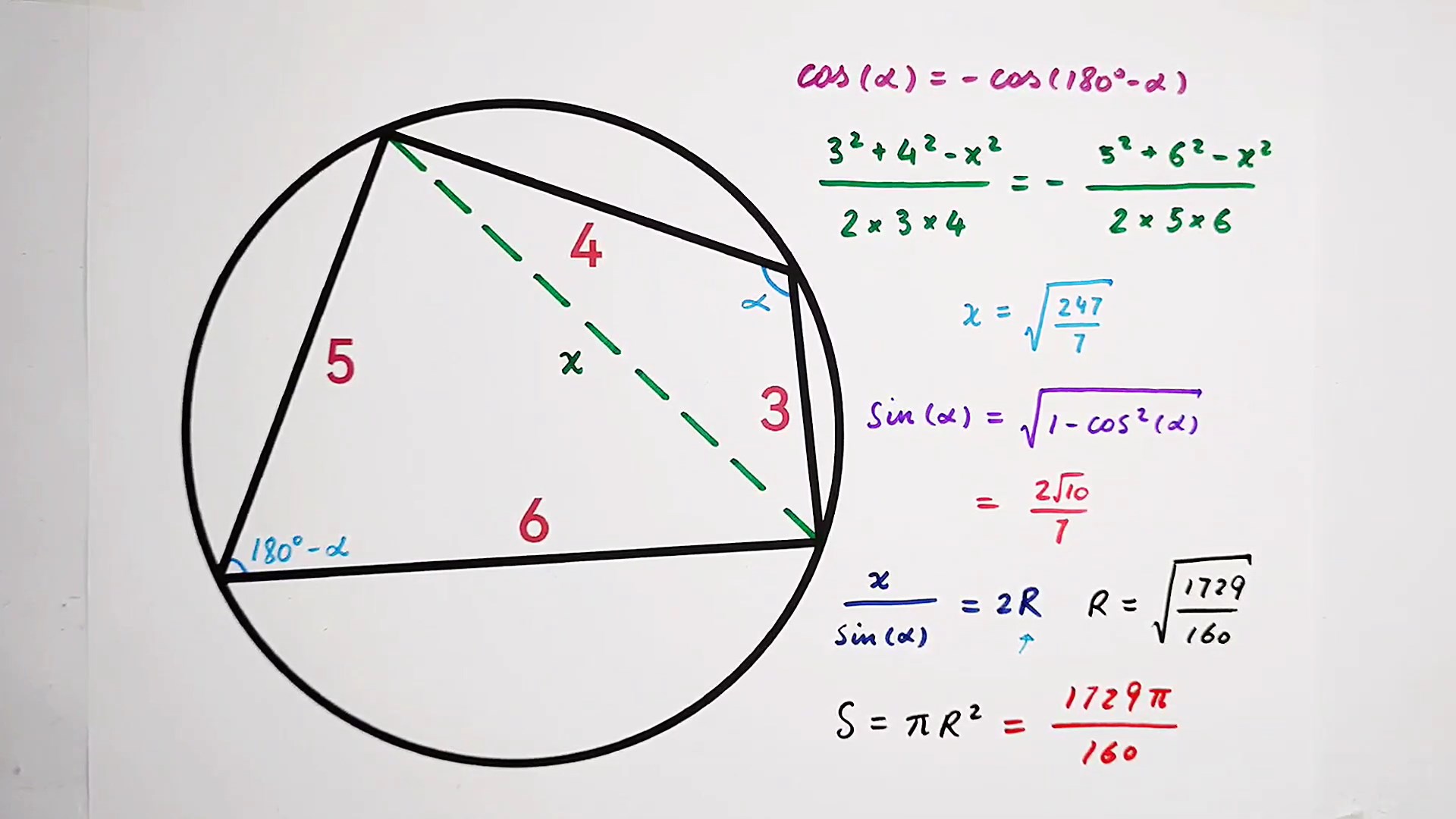
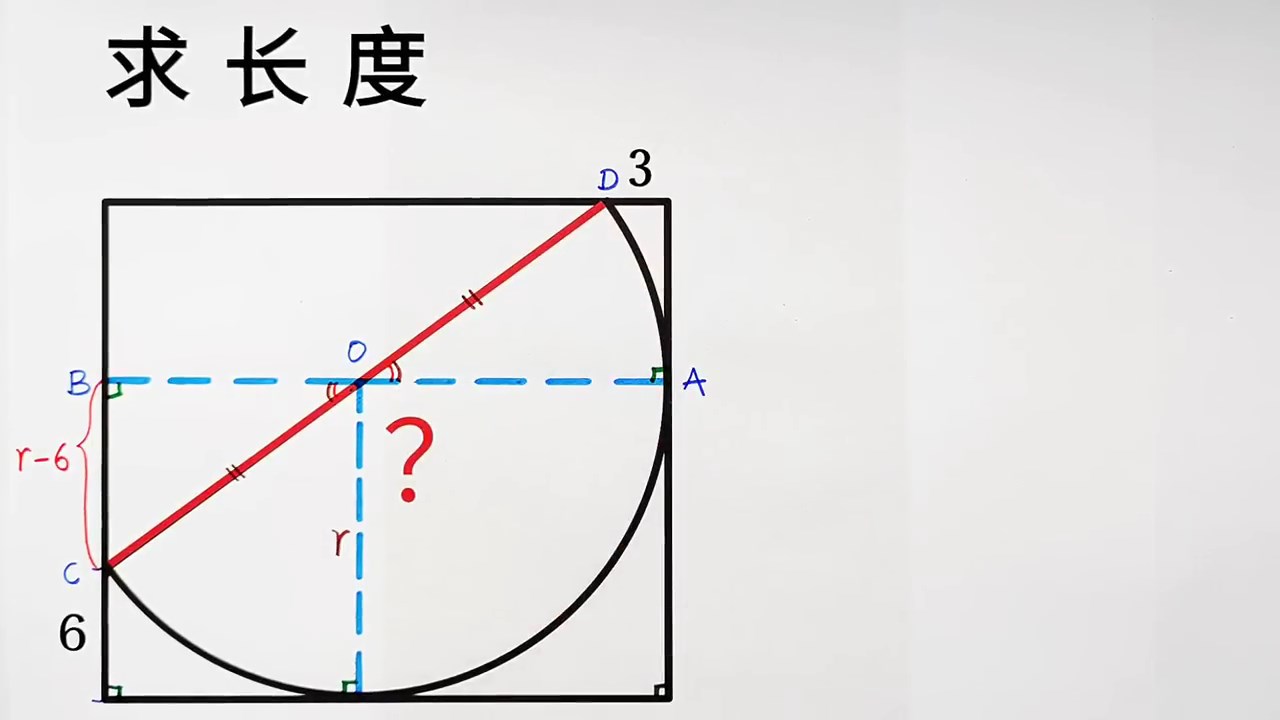
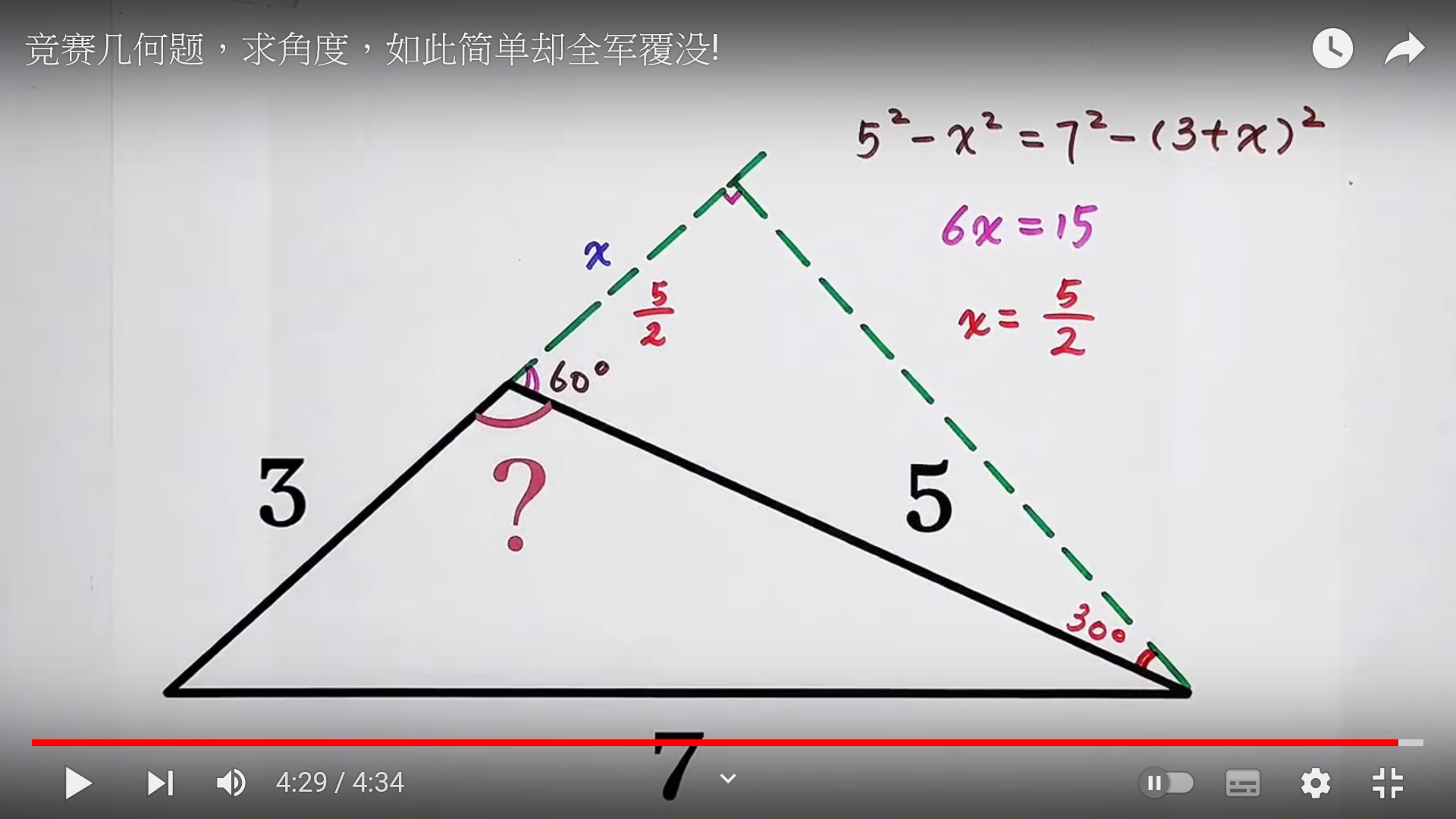
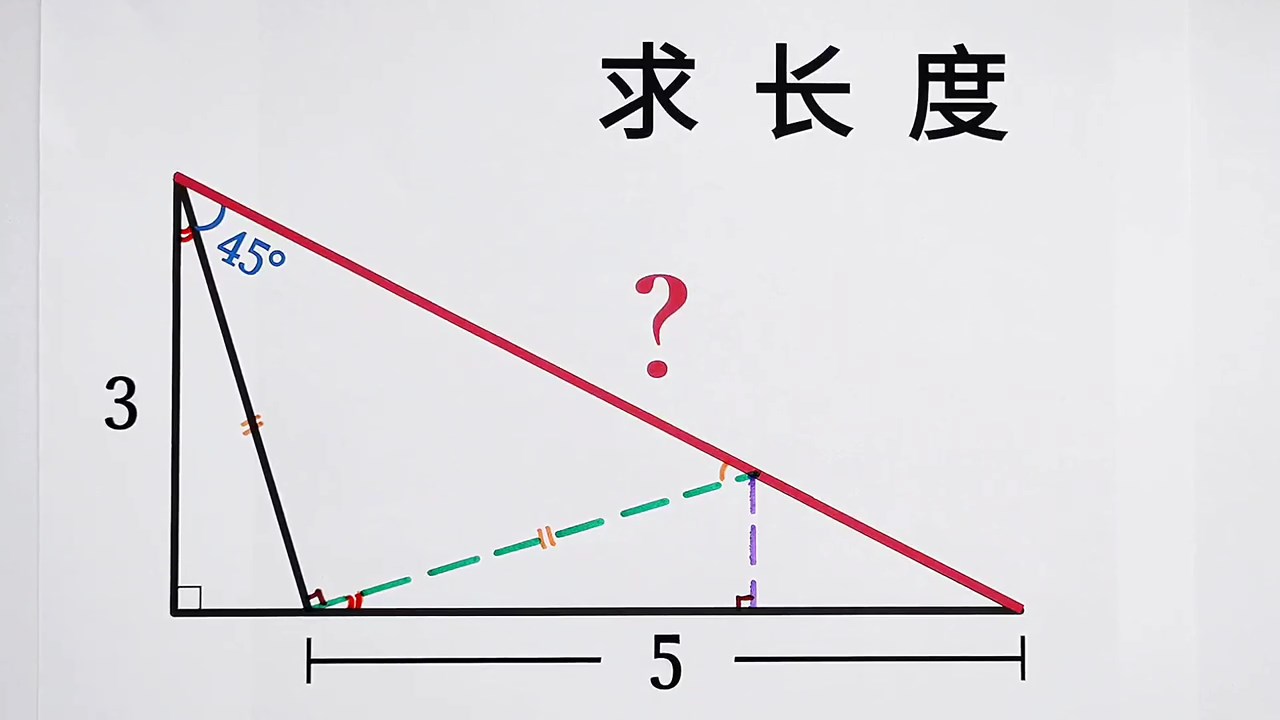

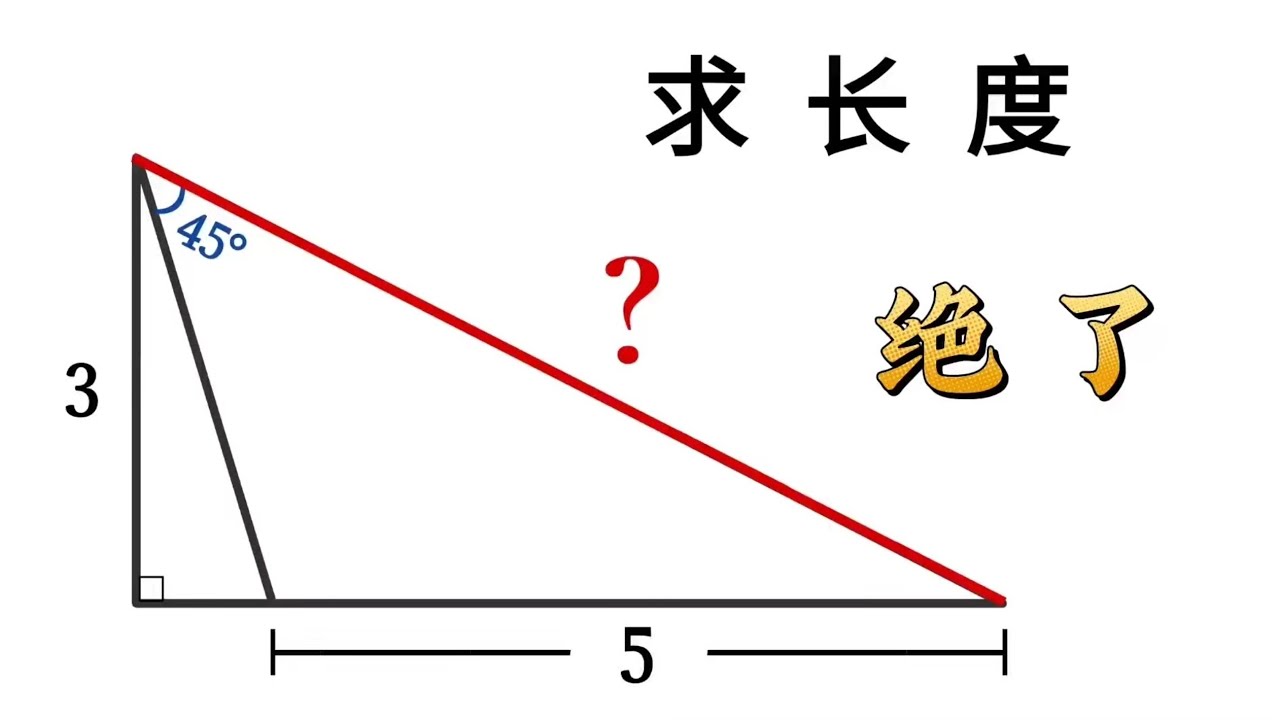
1:2+√3=2-√3:1
左側隱藏三角形為15°75°90°之直角三角形。
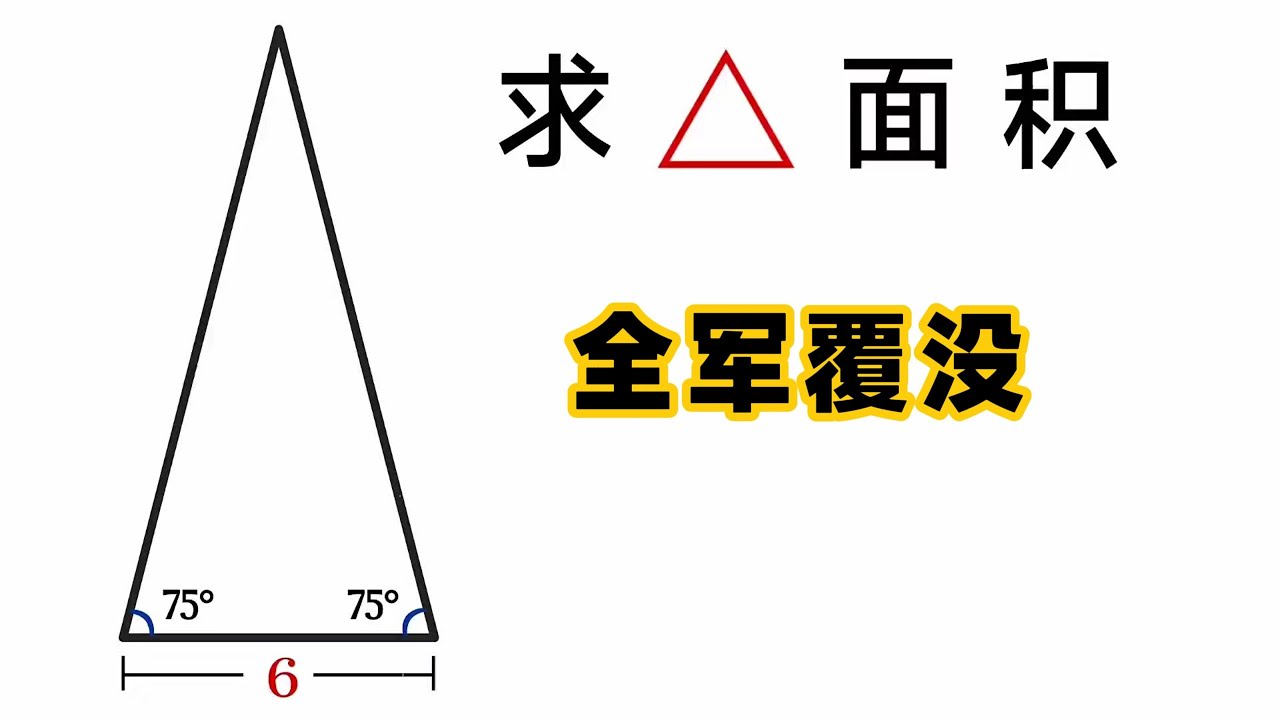
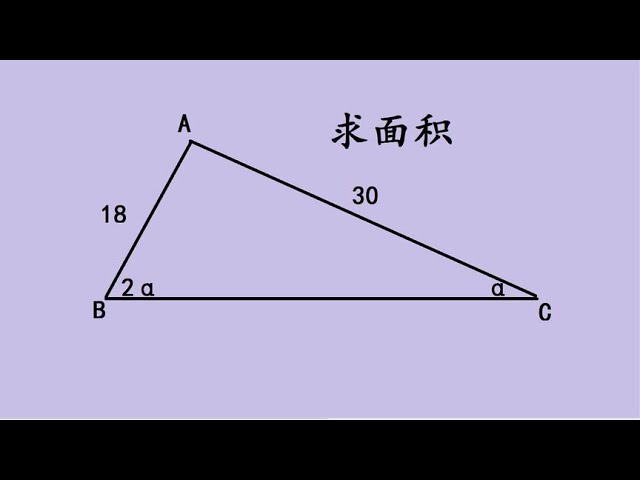
a 以 18 代入, b 以 30 代入,得出高為 5√11 , 18 為斜邊的直角三角形底為 7 ,大三角形底 32 ,面積 80√11 。
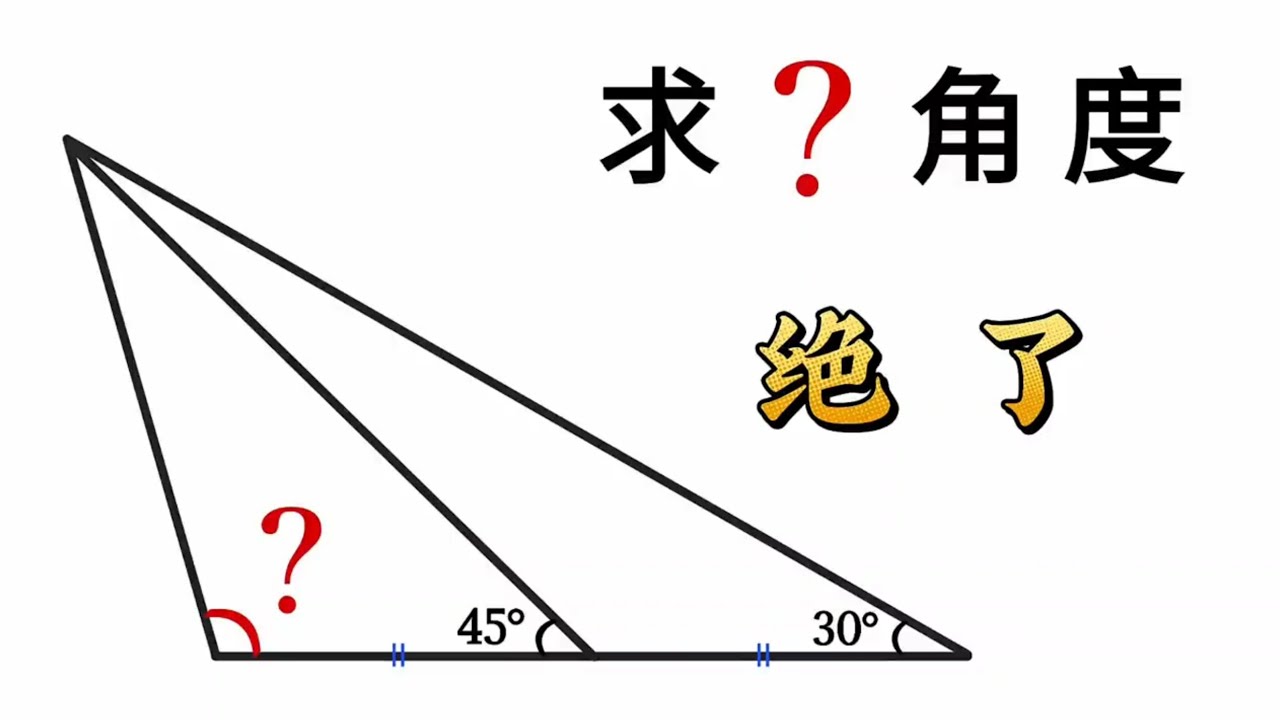
tanA=1/√3 ,求 tan2A ?
tan2A=2tanA/(1-tan2A)=√3, ∠A=30° ,2A=60° 。tanA=1/2 ,求 tan2A ?
tan2A=2tanA/(1-tan2A)=4/3 ,此為 3,4,5 三角形 。 2A 對 4 ,約 53.13° 。此分類目前未包含頁面或媒體。