分類:燒腦題：修訂版本之間的差異
（→中學數學題） |
（→中學數學題） |
||
| 第 53 行： | 第 53 行： | ||
</details> | </details> | ||
<details><summary>tanA=1/2 ，求 tan2A ？</summary> | <details><summary>tanA=1/2 ，求 tan2A ？</summary> | ||
| − | tan2A=2tanA/(1-tan<sup>2</sup>A)=4/3<br/> | + | tan2A=2tanA/(1-tan<sup>2</sup>A)=4/3 ，此為 3,4,5 三角形 。 2A 對 4 ，約 53.13° 。<br/> |
<img src='https://upload.wikimedia.org/wikipedia/commons/9/9e/Half-angle_formula_side_length_3_4_5.svg' width=400 height=* /> | <img src='https://upload.wikimedia.org/wikipedia/commons/9/9e/Half-angle_formula_side_length_3_4_5.svg' width=400 height=* /> | ||
</details> | </details> | ||
<details><summary><img src='http://jendo.org/files/解數學題/tan_2a.jpg' width=400 height=* /></summary> | <details><summary><img src='http://jendo.org/files/解數學題/tan_2a.jpg' width=400 height=* /></summary> | ||
| − | tan2A=2tanA/(1-tan<sup>2</sup>A)=3/4<br/> | + | tan2A=2tanA/(1-tan<sup>2</sup>A)=3/4 ，此為 3,4,5 三角形 。 2A 對 3 ，約 36.87° 。<br/> |
| + | ∠A=30° ，2A=60° 。 | ||
</details> | </details> | ||
'''因式分解：''' | '''因式分解：''' | ||
a<sup>5</sup>+a<sup>4</sup>+1 | a<sup>5</sup>+a<sup>4</sup>+1 | ||
2025年2月1日 (六) 13:49的修訂版本
求 a b
a2+b2=20 ，且 b 是 a 的小數部分。
|b|<1 且 b2 < 1
a2 > 19
設 a=n+b n為整數，且必為 ±4
(±4+b)2+b2=20
16±8b+2b2=20 => b2±4b-2=0
b=(∓4±√16+8)/2
b=∓2±√6
|b|<1 ，者 僅有 √6-2 ， 2-√6
a=4+b=√6+2 ， -(√6+2)
中學數學題
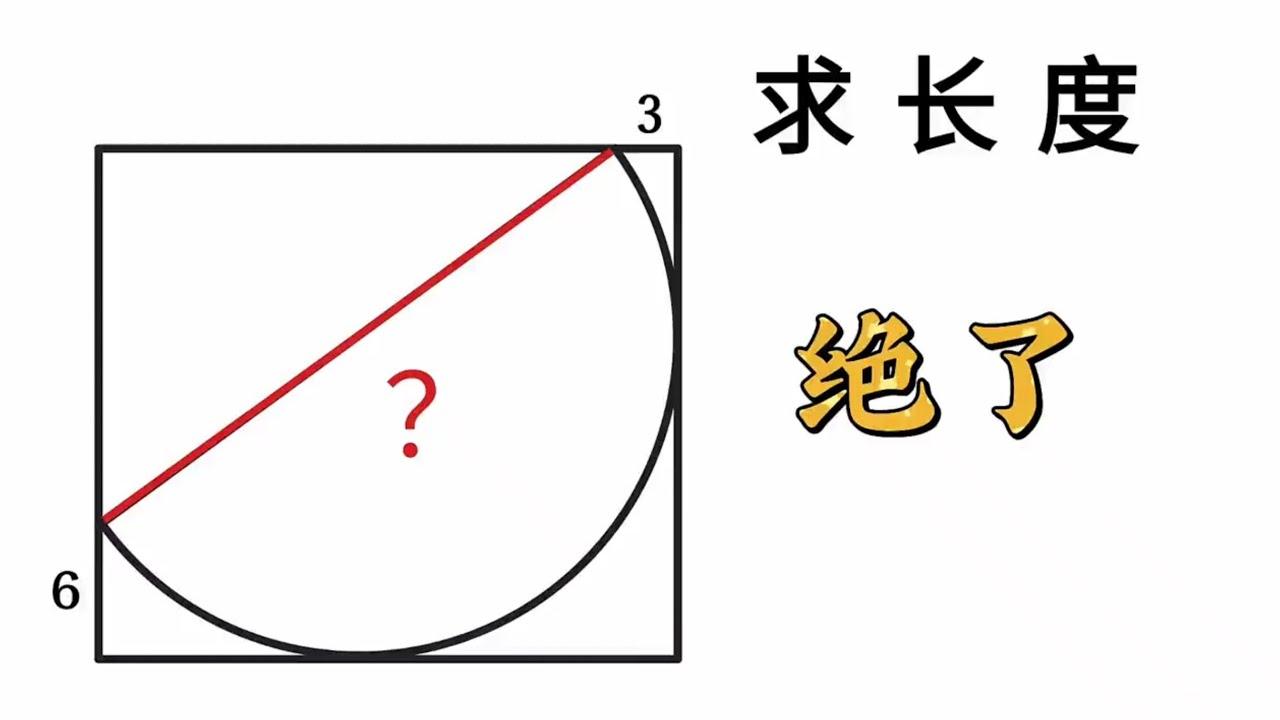
圓相關
圖半徑 R ，R-1.R-2,R 構成直角三角形
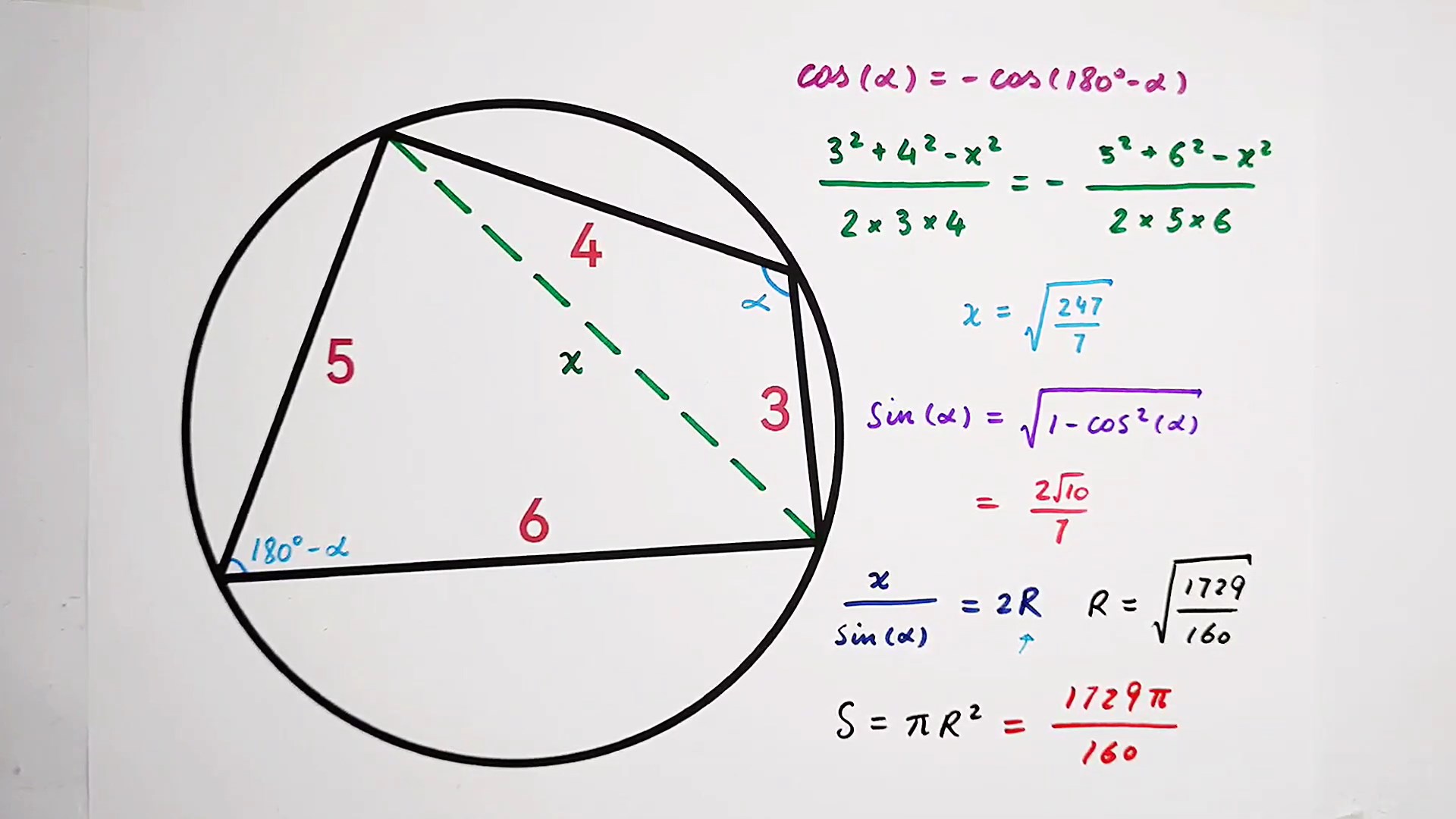
解出三邊為 3.4.5
兩圖相切，連心線過切點。左側中圖半徑 2 ，右側中圖半徑 r 。
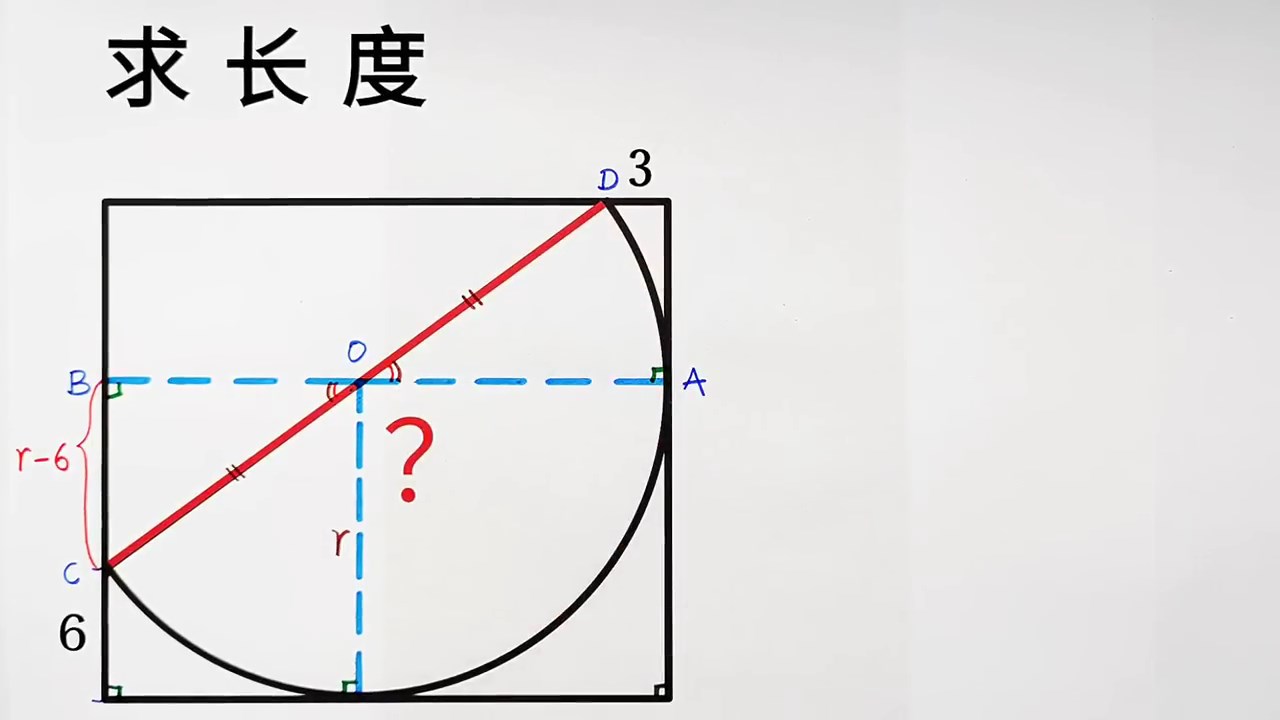
2,(4-r),(2+r) 構成直角三角形，解出 r 為 4/3 。
陰影三角形順時鐘轉 90° ，與 3,4,5 三角形同底等高。面積為 6 。
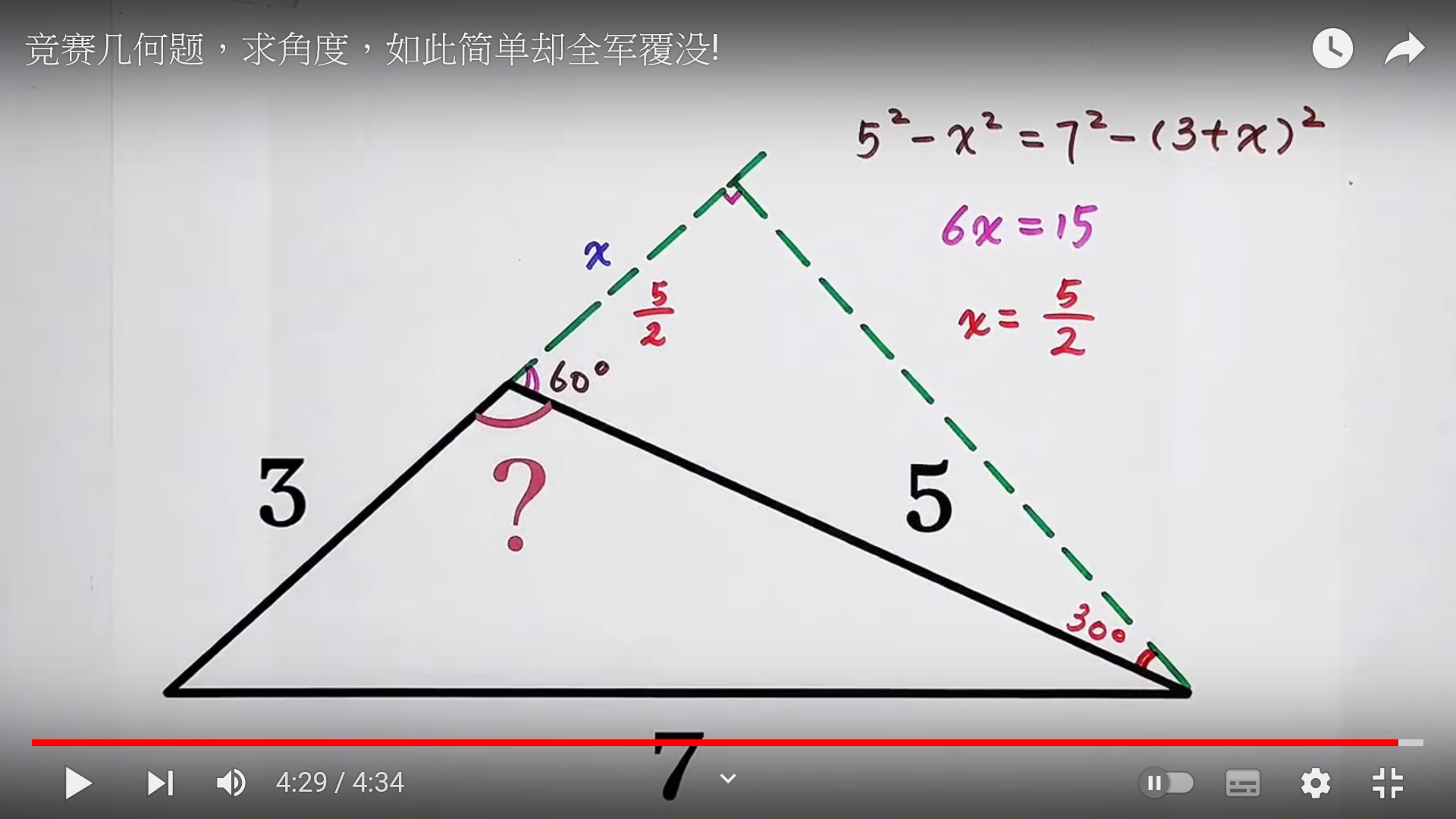
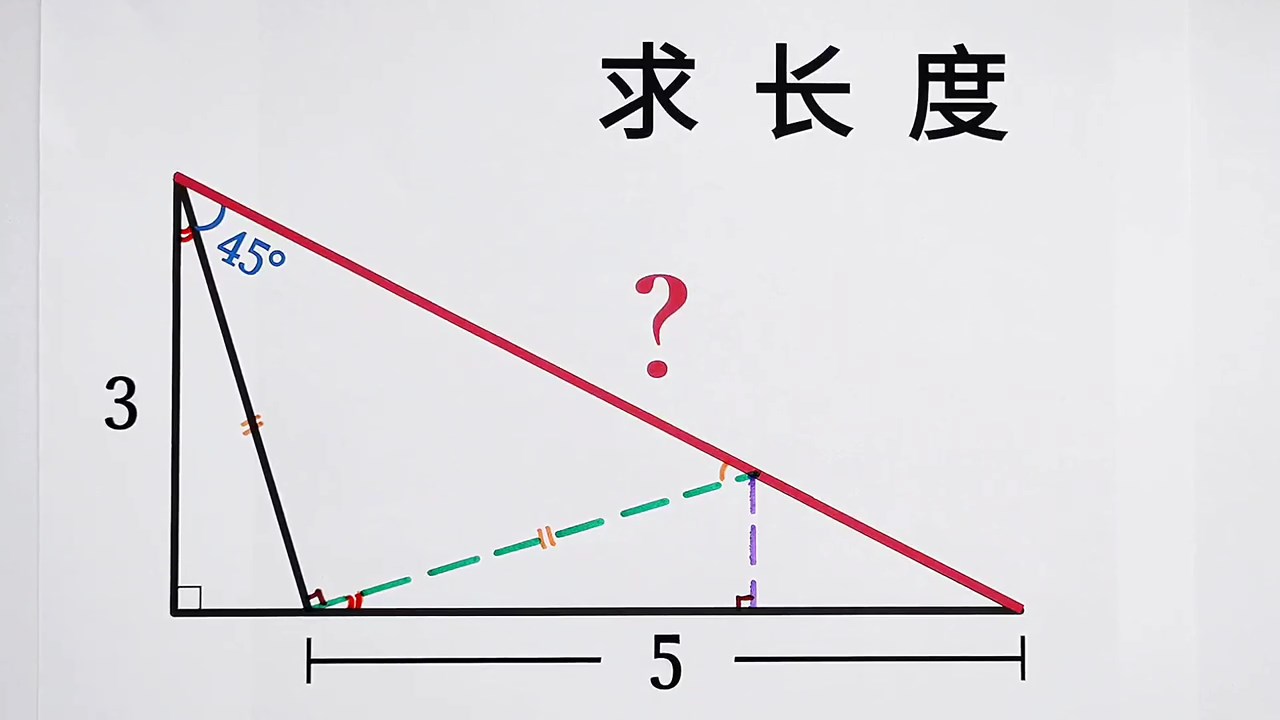
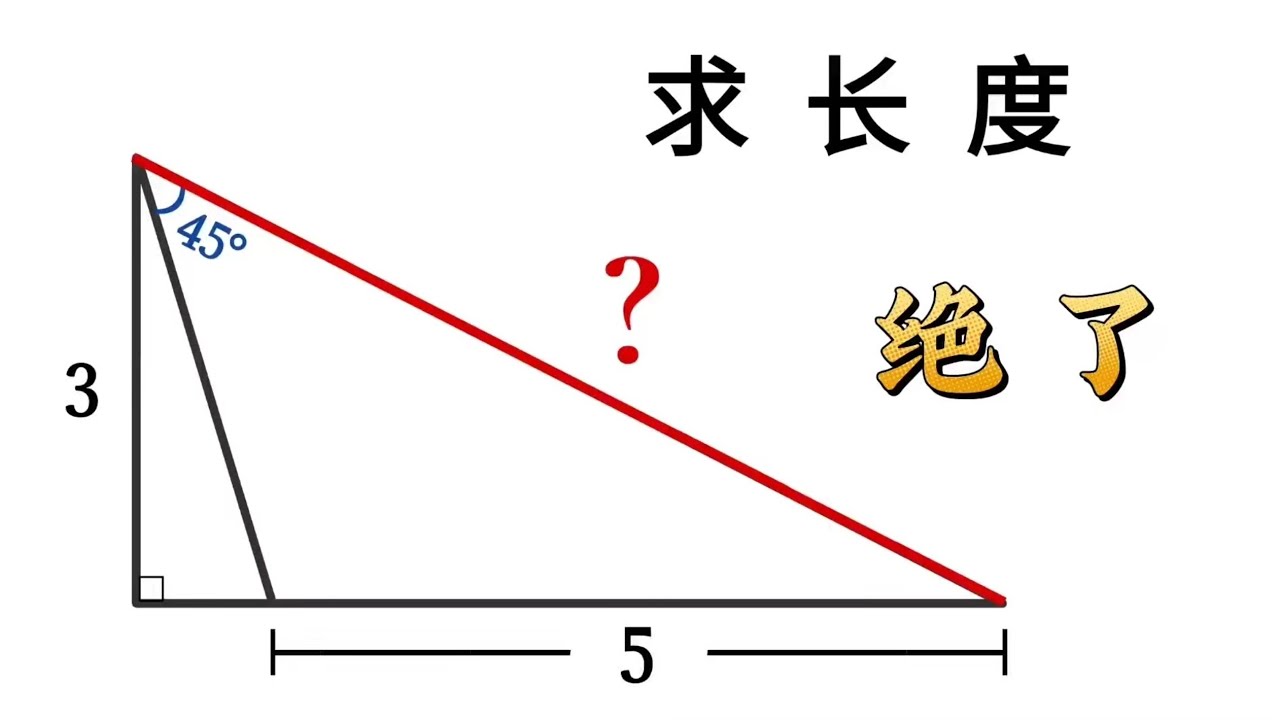
1:2+√3=2-√3:1
左側隱藏直角三角形之高為 1 ，兩個等長的底為 x ，左側隱藏直角三角形之底為(1-(√3-1))=2-√3
左側隱藏三角形為15°75°90°之直角三角形。
右側邊(18)垂直翻轉 180° 即成為典型的半角公式圖形。
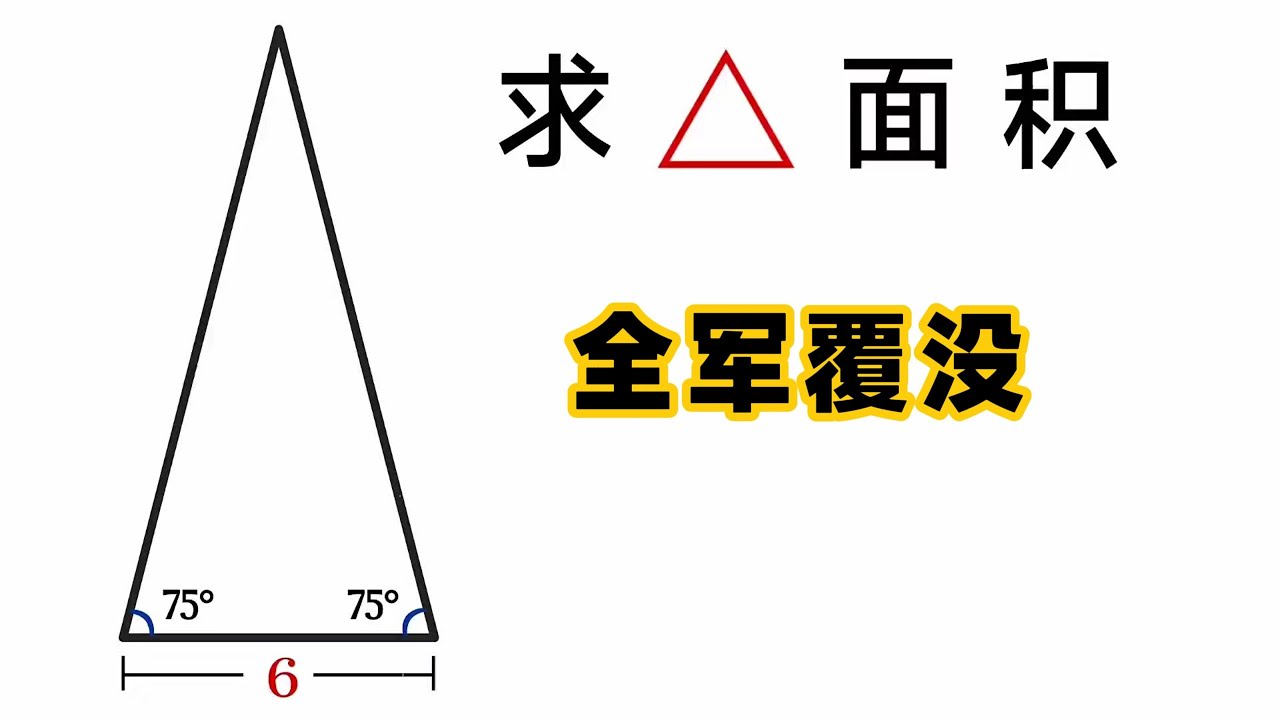
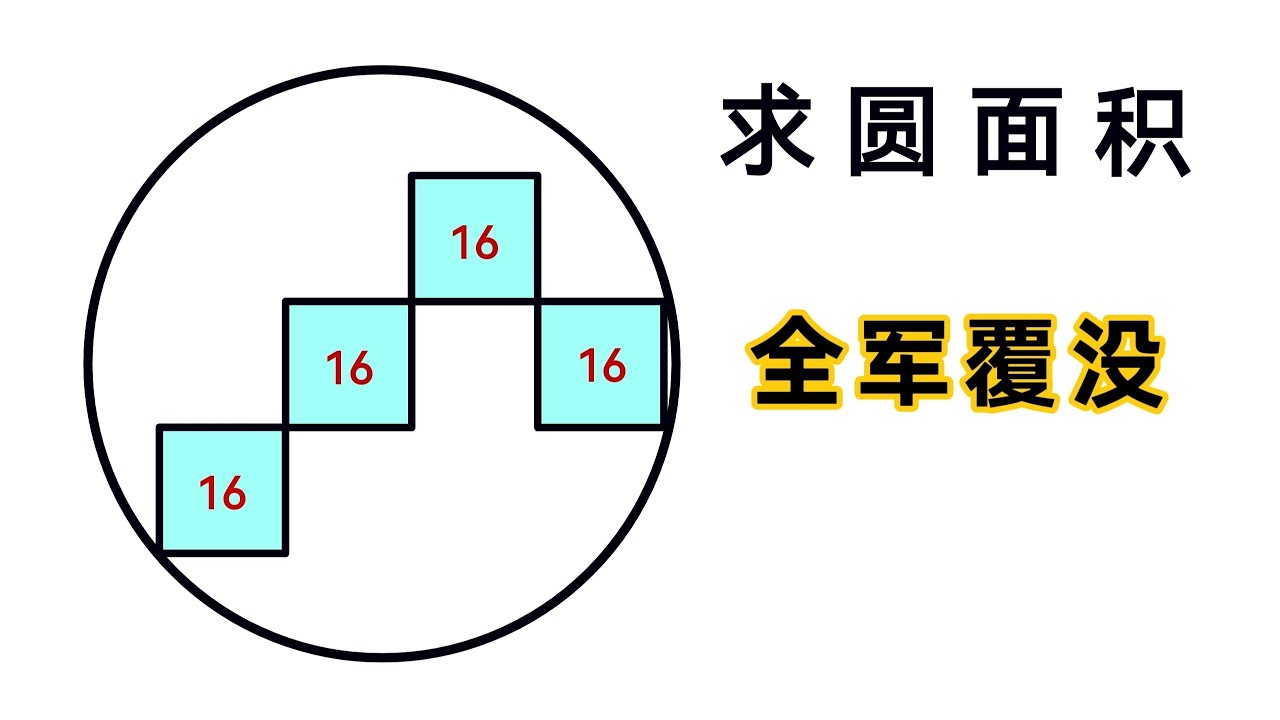
a 以 18 代入， b 以 30 代入，得出高為 5√11 ， 18 為斜邊的直角三角形底為 7 ，大三角形底 32 ，面積 80√11 。
tanA=1/√3 ，求 tan2A ？
tan2A=2tanA/(1-tan2A)=√3， ∠A=30° ，2A=60° 。
tanA=1/2 ，求 tan2A ？
tan2A=2tanA/(1-tan2A)=4/3 ，此為 3,4,5 三角形 。 2A 對 4 ，約 53.13° 。
tan2A=2tanA/(1-tan2A)=3/4 ，此為 3,4,5 三角形 。 2A 對 3 ，約 36.87° 。
∠A=30° ，2A=60° 。
此分類目前未包含頁面或媒體。
